우선순위 큐
- 높은 우선순위를 가진 원소를 먼저 처리하는 자료구조이다.
- 데이터를 우선순위에 따라 처리하고 싶을 때 사용한다.
구현 방법
- 리스트를 이용한 구현 : 삽입 시간 O(1), 삭제 시간 O(N)
- 힙(heap)을 이용한 구현 : 삽입 시간 O(logN), 삭제 시간 O(logN)
힙(Heap)의 특징
- 완전 이진 트리 자료구조의 일종
- 항상 루트 노드(root node)를 제거
- 최소 힙(min heap)
- 루트 노드가 가장 작은 값을 가진다.
- 따라서 값이 작은 데이터가 우선적으로 제거된다.
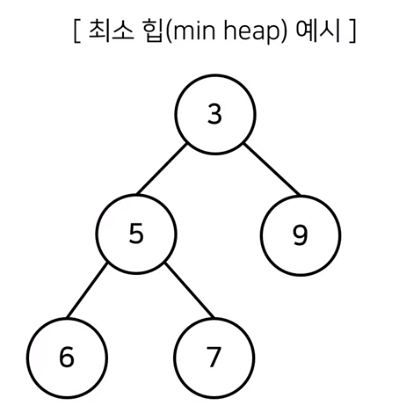
Heapq
- 최소 힙(min heap)의 구조
- 힙을 만들기 위해서는, 초기화된 리스트 [ ] 를 사용하거나(food = [ ]), heapify를 통해 값이 들어있는 리스트를 힙으로 변환
push
- item을 heap에 추가 (O(logN))
- 힙의 형태를 유지하면서 item을 push
heapq.heappush(heap, item)
heapq.heappush(heap, 10)
pop
- 힙의 형태를 유지하면서 가장 작은 항목을 삭제하고 반환 (O(logN))
- 비어있다면 IndexError 발생
- 반환하지 않고 접근하고 싶다면, heap[0] 이용 → a = heap[0]
heapq.heappop(heap)두번째로 작은 원소를 가져오고 싶다 → heap[1] X
heappop()으로 가장 작은 원소를 삭제 후에 heap[0] 으로 새로운 최솟값 찾기
heapify
- 원소가 들어있는 리스트를 즉각적으로 heap 자료형으로 반환 (O(N))
heapq.heapify(heaplist)
heappushpop
- 힙에 item을 푸시하고, heap에서 가장 작은 항목을 pop해 반환
heapq.heappushpop(heap, item)
튜플 형태로 heap을 다루고 싶다면?
for i in range(food_left):
heapq.heappush(food, (food_times[i], i+1))튜플의 첫 번째 원소를 우선순위로 힙을 구성하게 됨!
pop시에는 인덱싱을 통해 접근이 가능
heapq.heappop(heap)[1]
heapq.heappop(heap)[0]
최대 힙을 만들고 싶다면?
heap_items = [1,3,5,7,9]
max_heap = []
for item in heap_items:
heapq.heappush(max_heap, (-item, item))
print(max_heap) # [(-9, 9), (-7, 7), (-3, 3), (-1, 1), (-5, 5)]heapq.heappop(max_heap)[1] 을 하게 되면 힙의 최댓값이 반환됨!
참고 블로그, 강의 :
https://littlefoxdiary.tistory.com/3
https://velog.io/@mein-figur/Python%EC%9A%B0%EC%84%A0%EC%88%9C%EC%9C%84-%ED%81%90-heapq
https://www.youtube.com/watch?v=AjFlp951nz0&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=11
'CS > 알고리즘' 카테고리의 다른 글
| [이코테] 구현 - 기둥과 보 설치 (0) | 2023.02.28 |
|---|---|
| [이코테] 구현 - 뱀 (0) | 2023.02.28 |
| [이코테] 구현 - 문자열 압축 (1) | 2023.02.27 |
| [이코테] 그리디 - 무지의 먹방 라이브 (0) | 2023.02.27 |
| Python 정리해보기 (0) | 2023.02.15 |
우선순위 큐
- 높은 우선순위를 가진 원소를 먼저 처리하는 자료구조이다.
- 데이터를 우선순위에 따라 처리하고 싶을 때 사용한다.
구현 방법
- 리스트를 이용한 구현 : 삽입 시간 O(1), 삭제 시간 O(N)
- 힙(heap)을 이용한 구현 : 삽입 시간 O(logN), 삭제 시간 O(logN)
힙(Heap)의 특징
- 완전 이진 트리 자료구조의 일종
- 항상 루트 노드(root node)를 제거
- 최소 힙(min heap)
- 루트 노드가 가장 작은 값을 가진다.
- 따라서 값이 작은 데이터가 우선적으로 제거된다.

Heapq
- 최소 힙(min heap)의 구조
- 힙을 만들기 위해서는, 초기화된 리스트 [ ] 를 사용하거나(food = [ ]), heapify를 통해 값이 들어있는 리스트를 힙으로 변환
push
- item을 heap에 추가 (O(logN))
- 힙의 형태를 유지하면서 item을 push
heapq.heappush(heap, item)
heapq.heappush(heap, 10)
pop
- 힙의 형태를 유지하면서 가장 작은 항목을 삭제하고 반환 (O(logN))
- 비어있다면 IndexError 발생
- 반환하지 않고 접근하고 싶다면, heap[0] 이용 → a = heap[0]
heapq.heappop(heap)두번째로 작은 원소를 가져오고 싶다 → heap[1] X
heappop()으로 가장 작은 원소를 삭제 후에 heap[0] 으로 새로운 최솟값 찾기
heapify
- 원소가 들어있는 리스트를 즉각적으로 heap 자료형으로 반환 (O(N))
heapq.heapify(heaplist)
heappushpop
- 힙에 item을 푸시하고, heap에서 가장 작은 항목을 pop해 반환
heapq.heappushpop(heap, item)
튜플 형태로 heap을 다루고 싶다면?
for i in range(food_left):
heapq.heappush(food, (food_times[i], i+1))튜플의 첫 번째 원소를 우선순위로 힙을 구성하게 됨!
pop시에는 인덱싱을 통해 접근이 가능
heapq.heappop(heap)[1]
heapq.heappop(heap)[0]
최대 힙을 만들고 싶다면?
heap_items = [1,3,5,7,9]
max_heap = []
for item in heap_items:
heapq.heappush(max_heap, (-item, item))
print(max_heap) # [(-9, 9), (-7, 7), (-3, 3), (-1, 1), (-5, 5)]heapq.heappop(max_heap)[1] 을 하게 되면 힙의 최댓값이 반환됨!
참고 블로그, 강의 :
https://littlefoxdiary.tistory.com/3
https://velog.io/@mein-figur/Python%EC%9A%B0%EC%84%A0%EC%88%9C%EC%9C%84-%ED%81%90-heapq
https://www.youtube.com/watch?v=AjFlp951nz0&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=11
'CS > 알고리즘' 카테고리의 다른 글
| [이코테] 구현 - 기둥과 보 설치 (0) | 2023.02.28 |
|---|---|
| [이코테] 구현 - 뱀 (0) | 2023.02.28 |
| [이코테] 구현 - 문자열 압축 (1) | 2023.02.27 |
| [이코테] 그리디 - 무지의 먹방 라이브 (0) | 2023.02.27 |
| Python 정리해보기 (0) | 2023.02.15 |
