목차
우선순위 큐 ADT
- 항목(키, 원소)들을 저장
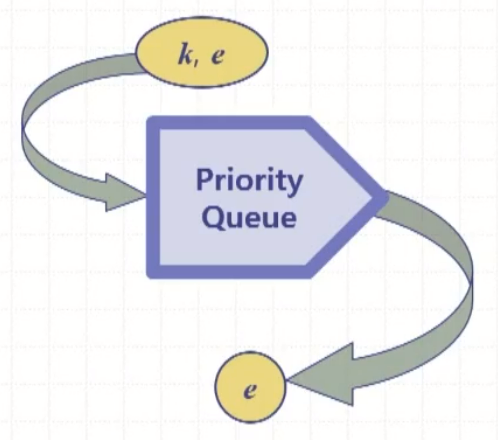
우선순위 큐 ADT 메서드
- 주요 메서드
- insertItem(k, e): 키 k인 원소 e를 큐에 삽입
- element removeMin(): 큐로부터 최소 키를 가진 원소를 삭제하여 반환
- 일반 메서드
- integer size(): 큐의 항목 수를 반환
- boolean isEmpty(): 큐가 비어 있는지 여부를 반환
- 접근 메서드
- element minElement(): 큐에서 최소 키를 가진 원소를 반환
- element minkey(): 큐에서 최소 키를 반환
- 예외
- emptyQueueException(): 비어 있는 큐에 대해 삭제나 원소 접근을 시도할 경우 발령
- fullQueueException(): 만원 큐에 대해 삽입을 시도할 경우 발령
우선순위 큐를 이용한 정렬
- 비교 가능한 원소 집합을 정렬하는 데 우선순위 큐 이용
- 연속적인 insertItem(e, e) 작업을 통해 원소들을 하나씩 삽입 (key = e로 전제, e는 정렬 기준 ex) 키)
- 연속적인 removeMin() 작업을 통해 원소들을 정렬 순서로 삭제
- 실행시간: 우선순위 큐의 구현에 따라 다르다
- L, P: 일반(generic) - (배열, 연결리스트 등 일반적으로 이용 가능)
Alg PQ-Sort(L)
input list L
output sorted list L
1. P <- empty priority queue
2. while (!LisEmpty())
e <- L.removeFirst()
P.insertItem(e)
3. while (!P.isEmpty())
e <- P.removeMin()
L.addLast(e)
4. return
리스트에 기초한 우선순위 큐
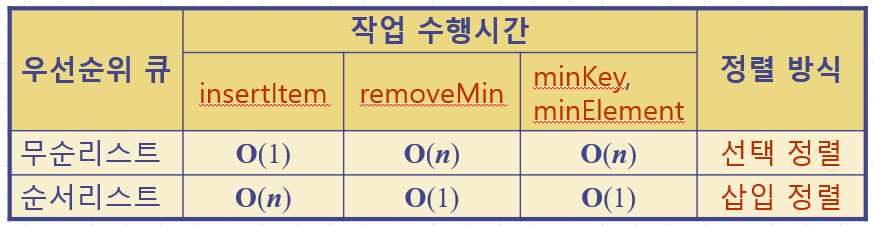
무순리스트로 구현 (선택 정렬)
- 우선순위 큐의 항목들을 리스트에 임의 순서로 저장
- 성능
- insertItem: O(1) 시간 소요 - 항목을 리스트의 맨앞 또는 맨뒤에 삽입할 수 있으므로
- removeMin, minKey, minElement: O(n) 시간 소요 - 최소 키를 찾기 위해 전체 리스트를 순회해야 하므로
순서리스트로 구현 (삽입 정렬)
- 우선순위 큐의 항목들을 리스트에 키 정렬 순서로 저장
- 성능
- insertItem: O(n) 시간 소요 - 항목을 삽입할 곳을 찾아야 하므로
- removeMin, minKey, minElement: O(1) 시간 소요 - 최소 키가 리스트의 맨앞에 있으므로
선택 정렬 (selection-sort)
- PQ-Sort의 일종
- 우선순위 큐를 무순리스트로 구현
- 실행시간
- n회의 insertItem 작업을 사용하여 원소들을 우선순위 큐에 삽입하는데 O(n) 시간 소요
- n회의 removeMin 작업을 사용하여 원소들을 우선순위 큐로부터 정렬 순서로 삭제하는데 다음의 비례하는 시간 소요 → n + (n - 1) + (n - 2) + ... + 2 + 1
- Total: O(n^2)
삽입 정렬 (insertion-sort)
- PQ-Sort의 일종
- 우선순위 큐를 순서리스트로 구현
- 실행시간
- n회의 insertItem 작업을 사용하여 원소들을 우선순위 큐에 삽입하는데 다음에 비례하는 시간 소요 → 0 + 1 + 2 + ... + (n - 2) + (n - 1) + n
- n회의 removeMin 작업을 사용하여 원소들을 우선순위 큐로부터 정렬 순서로 삭제하는데 O(n) 시간 소요
- Total: O(n^2)
제자리에서 할 수 있나?
- selection-sort, insertion-sort 모두 O(n) 공간을 차지하는 외부의 우선순위 큐를 사용하여 리스트를 정렬
- 원래 리스트 자체를 위한 공간 이외에 O(1) 공간만을 사용한다면 제자리(in-place)에서 수행한다고 함
- 일반적으로, 어떤 정렬 알고리즘이 정렬 대상 개체를 위해 필요한 메모리에 추가하여 오직 상수 메모리만을 사용한다면, 해당 정렬 알고리즘이 제자리에서 수행한다고 말함
제자리 선택 정렬
- selection-sort가 외부 데이터구조를 사용하는 대신, 제자리에서 수행하도록 구현 가능
- 우선순위 큐: 입력 리스트의 일부
- In-place selection-sort를 위해서는
- 리스트의 앞부분을 정렬 상태로 유지
- 리스트를 변경하는 대신 swapElements를 사용
제자리 삽입 정렬
- insertion-sort가 외부 데이터구조를 사용하는 대신, 제자리에서 수행하도록 구현 가능
- 우선순위 큐: 입력 리스트의 일부
- in-place insertion-sort를 위해서는
- 리스트의 앞부분을 정렬 상태로 유지
- 리스트를 변경하는 대신 swapElements를 사용
Alg inPlaceSelectionSort(A)
input array A of n keys
output sorted array A
1. for pass <- 0 to n-2 // O(n)
minLoc <- pass
for j <- (pass + 1) to n-1 // O(n)
if (A[j] < A[minLoc])
minLoc <- j
A[pass] <-> A[minLoc]
2. return
Alg inPlaceInsertionSort(A)
input array A of n keys
output sorted array A
1. for pass <- 1 to n-1 // O(n)
save <- A[pass]
j <- pass-1
while((j>=0) & (A[j]>save)) // O(n)
A[j+1] <- A[j]
j <- j-1
A[j+1] <- save
2. return
선택 정렬 vs 삽입 정렬
- 공통점
- 전체적으로 O(n^2) 시간
- 내부 반복문: O(n) 선형 탐색
- 외부 반복문: O(n) 패스
- 제자리 버전은 O(1) 공간 소요
- 구현이 단순
- 작은 n에 대해 유용
- 전체적으로 O(n^2) 시간
- 초기 리스트가 완전히 또는 거의 정렬된 경우
- in-place insertion-sort가 더 빠르다
- 내부 반복문이 O(1) 시간 소요 - 따라서 전체적으로 O(n) 시간에 수행되므로
- swapElements 작업이 비싼 경우
- in-place selection-sort가 더 빠르다.
- swapElements 작업이 패스마다 O(1) 시간 수행되는데 반해, in-place insertion-sort에서는 동일 작업이 패스마다 최악의 경우 O(n) 시간 수행되므로
'CS > 알고리즘' 카테고리의 다른 글
| 합병 정렬, 퀵 정렬 (0) | 2023.09.27 |
|---|---|
| 힙과 힙 정렬 (2) | 2023.09.19 |
| 해시(Hash) - Dictionary (0) | 2023.07.07 |
| [프로그래머스] 그리디 - 큰 수 만들기 (0) | 2023.06.27 |
| [Python] sys.stdin.readline().strip() (0) | 2023.06.24 |
우선순위 큐 ADT
- 항목(키, 원소)들을 저장

우선순위 큐 ADT 메서드
- 주요 메서드
- insertItem(k, e): 키 k인 원소 e를 큐에 삽입
- element removeMin(): 큐로부터 최소 키를 가진 원소를 삭제하여 반환
- 일반 메서드
- integer size(): 큐의 항목 수를 반환
- boolean isEmpty(): 큐가 비어 있는지 여부를 반환
- 접근 메서드
- element minElement(): 큐에서 최소 키를 가진 원소를 반환
- element minkey(): 큐에서 최소 키를 반환
- 예외
- emptyQueueException(): 비어 있는 큐에 대해 삭제나 원소 접근을 시도할 경우 발령
- fullQueueException(): 만원 큐에 대해 삽입을 시도할 경우 발령
우선순위 큐를 이용한 정렬
- 비교 가능한 원소 집합을 정렬하는 데 우선순위 큐 이용
- 연속적인 insertItem(e, e) 작업을 통해 원소들을 하나씩 삽입 (key = e로 전제, e는 정렬 기준 ex) 키)
- 연속적인 removeMin() 작업을 통해 원소들을 정렬 순서로 삭제
- 실행시간: 우선순위 큐의 구현에 따라 다르다
- L, P: 일반(generic) - (배열, 연결리스트 등 일반적으로 이용 가능)
Alg PQ-Sort(L)
input list L
output sorted list L
1. P <- empty priority queue
2. while (!LisEmpty())
e <- L.removeFirst()
P.insertItem(e)
3. while (!P.isEmpty())
e <- P.removeMin()
L.addLast(e)
4. return
리스트에 기초한 우선순위 큐
무순리스트로 구현 (선택 정렬)
- 우선순위 큐의 항목들을 리스트에 임의 순서로 저장
- 성능
- insertItem: O(1) 시간 소요 - 항목을 리스트의 맨앞 또는 맨뒤에 삽입할 수 있으므로
- removeMin, minKey, minElement: O(n) 시간 소요 - 최소 키를 찾기 위해 전체 리스트를 순회해야 하므로
순서리스트로 구현 (삽입 정렬)
- 우선순위 큐의 항목들을 리스트에 키 정렬 순서로 저장
- 성능
- insertItem: O(n) 시간 소요 - 항목을 삽입할 곳을 찾아야 하므로
- removeMin, minKey, minElement: O(1) 시간 소요 - 최소 키가 리스트의 맨앞에 있으므로
선택 정렬 (selection-sort)
- PQ-Sort의 일종
- 우선순위 큐를 무순리스트로 구현
- 실행시간
- n회의 insertItem 작업을 사용하여 원소들을 우선순위 큐에 삽입하는데 O(n) 시간 소요
- n회의 removeMin 작업을 사용하여 원소들을 우선순위 큐로부터 정렬 순서로 삭제하는데 다음의 비례하는 시간 소요 → n + (n - 1) + (n - 2) + ... + 2 + 1
- Total: O(n^2)
삽입 정렬 (insertion-sort)
- PQ-Sort의 일종
- 우선순위 큐를 순서리스트로 구현
- 실행시간
- n회의 insertItem 작업을 사용하여 원소들을 우선순위 큐에 삽입하는데 다음에 비례하는 시간 소요 → 0 + 1 + 2 + ... + (n - 2) + (n - 1) + n
- n회의 removeMin 작업을 사용하여 원소들을 우선순위 큐로부터 정렬 순서로 삭제하는데 O(n) 시간 소요
- Total: O(n^2)
제자리에서 할 수 있나?
- selection-sort, insertion-sort 모두 O(n) 공간을 차지하는 외부의 우선순위 큐를 사용하여 리스트를 정렬
- 원래 리스트 자체를 위한 공간 이외에 O(1) 공간만을 사용한다면 제자리(in-place)에서 수행한다고 함
- 일반적으로, 어떤 정렬 알고리즘이 정렬 대상 개체를 위해 필요한 메모리에 추가하여 오직 상수 메모리만을 사용한다면, 해당 정렬 알고리즘이 제자리에서 수행한다고 말함
제자리 선택 정렬
- selection-sort가 외부 데이터구조를 사용하는 대신, 제자리에서 수행하도록 구현 가능
- 우선순위 큐: 입력 리스트의 일부
- In-place selection-sort를 위해서는
- 리스트의 앞부분을 정렬 상태로 유지
- 리스트를 변경하는 대신 swapElements를 사용
제자리 삽입 정렬
- insertion-sort가 외부 데이터구조를 사용하는 대신, 제자리에서 수행하도록 구현 가능
- 우선순위 큐: 입력 리스트의 일부
- in-place insertion-sort를 위해서는
- 리스트의 앞부분을 정렬 상태로 유지
- 리스트를 변경하는 대신 swapElements를 사용
Alg inPlaceSelectionSort(A)
input array A of n keys
output sorted array A
1. for pass <- 0 to n-2 // O(n)
minLoc <- pass
for j <- (pass + 1) to n-1 // O(n)
if (A[j] < A[minLoc])
minLoc <- j
A[pass] <-> A[minLoc]
2. return
Alg inPlaceInsertionSort(A)
input array A of n keys
output sorted array A
1. for pass <- 1 to n-1 // O(n)
save <- A[pass]
j <- pass-1
while((j>=0) & (A[j]>save)) // O(n)
A[j+1] <- A[j]
j <- j-1
A[j+1] <- save
2. return
선택 정렬 vs 삽입 정렬
- 공통점
- 전체적으로 O(n^2) 시간
- 내부 반복문: O(n) 선형 탐색
- 외부 반복문: O(n) 패스
- 제자리 버전은 O(1) 공간 소요
- 구현이 단순
- 작은 n에 대해 유용
- 전체적으로 O(n^2) 시간
- 초기 리스트가 완전히 또는 거의 정렬된 경우
- in-place insertion-sort가 더 빠르다
- 내부 반복문이 O(1) 시간 소요 - 따라서 전체적으로 O(n) 시간에 수행되므로
- swapElements 작업이 비싼 경우
- in-place selection-sort가 더 빠르다.
- swapElements 작업이 패스마다 O(1) 시간 수행되는데 반해, in-place insertion-sort에서는 동일 작업이 패스마다 최악의 경우 O(n) 시간 수행되므로

'CS > 알고리즘' 카테고리의 다른 글
| 합병 정렬, 퀵 정렬 (0) | 2023.09.27 |
|---|---|
| 힙과 힙 정렬 (2) | 2023.09.19 |
| 해시(Hash) - Dictionary (0) | 2023.07.07 |
| [프로그래머스] 그리디 - 큰 수 만들기 (0) | 2023.06.27 |
| [Python] sys.stdin.readline().strip() (0) | 2023.06.24 |
