목차
분할통치법 (divide-and-conquer)
- 일반적인 알고리즘 설계 기법의 일종
- 분할 (divide): 입력 데이터 L을 둘 이상의 분리된 부분집합 L1, L2, ... 으로 나눔
- 재귀 (recur): L1, L2, ... 각각에 대한 부문제를 재귀적으로 해결
- 통치 (conquer): 부문제들에 대한 해결을 합쳐 L의 해결을 구함
- 재귀의 베이스 케이스: 상수 크기의 부문제들
- 점화식 (recurrence equations)을 사용하여 분석
- ex) 합병 정렬 (merge-sort), 퀵 정렬 (quick-sort)
합병 정렬
- 합병 정렬 (merge-sort): 분할통치법에 기초한 정렬 알고리즘
- 힙 정렬(heap-sort)처럼
- 비교에 기초한 정렬
- O(nlogn) 시간에 수행
- 힙 정렬(heap-sort)과는 달리
- 외부의 우선순위 큐를 사용하지 않음
- 데이터를 순차적 방식으로 접근 (따라서 디스크의 데이터를 정렬하기에 적당)
- n개의 원소로 이루어진 입력 리스트 L에 대한 합병 정렬 (merge-sort)의 세 단계
- 분할 (divide): 무순리스트 L을 각각 n/2개의 원소를 가진 두 개의 부리스트 L1과 L2로 분할
- 재귀 (recur): L1과 L2를 각각 재귀적으로 정렬
- 통치 (conquer): L1과 L2를 단일 순서리스트로 합병
Alg mergeSort(L)
input list L with n elements
output sorted list L
1. if (L.size() > 1)
L1, L2 <- partition(L, n/2)
mergeSort(L1)
mergeSort(L2)
L <- merge(L1, L2)
2. return
두 개의 정렬 리스트 합병하기
- merge-sort의 통치 단계: 두 개의 정렬된 리스트 L1과 L2를 L1과 L2의 원소들의 합을 포함하는 정렬 리스트 L로 합병하는 과정
- 각각 n/2개의 원소를 가지며, 이중연결리스트로 구현된 두 개의 정렬 리스트를 합병하는데 O(n) 시간 소요
Alg merge(L1, L2)
input sorted list L1 and L2 with n/2 elements each
output sorted list of L1 U L2
1. L <- empty list
2. while (!L1.isEmpty() & !L2.isEmpty())
if (L1.get(1) <= L2.get(1))
L.addLast(L1.removeFirst())
else
L.addLast(L2.removeFirst())
3. while (!L1.isEmpty())
L.addLast(L1.removeFirst())
4. while (!L2.isEmpty())
L.addLast(L2.removeFirst())
5. return L
합병정렬 트리
- merge-sort의 실행을 이진트리로 도식화
- 이진트리의 각 노드는 merge-sort의 재귀호출을 표현하며 다음을 저장
- 실행 이전의 무순리스트 및 분할
- 실행 이후의 정렬리스트
- 루트는 초기 호출을 의미
- 잎들은 크기 1의 부리스트에 대한 호출을 의미
- 이진트리의 각 노드는 merge-sort의 재귀호출을 표현하며 다음을 저장
합병 정렬 분석
- 합병 정렬 트리의 높이 h: O(log n)
- 각 재귀호출에서 리스트를 절반으로 나누기 때문
- 깊이 i의 노드들에서 이루어지는 총 작업량: O(n)
- 2^i개의 크기 n/(2^i)의 리스트들을 분할하고 합병하기 때문
- 2^(k+1)번의 재귀호출 발생
- 따라서, merge-sort의 전체 실행시간: O(nlog n)
- 점화식으로도 해결 가능
- T(n) = c (n < 2)
- T(n) = 2T(n/2) + O(n) (n >= 2)
- 전체 실행시간: T(n) = O(nlog n)
배열에 대한 합병 정렬
- 배열에 대해 작동하는 merge-sort 알고리즘
- mergeSort(A): n개의 원소로 구성된 배열 A를 합병 정렬
- 힌트: 외부 배열을 "버퍼", 즉 임시 저장 공간으로 사용
Alg mergeSort(A)
input array A of n keys
output sorted array A
1. rMergeSort(A, 0, n-1)
2. returnAlg rMergeSort(A, l, r)
input array A[l..r]
output sorted array A[l..r]
1. if (l < r)
m <- floor((l+r)/2)
rMergeSort(A, l, m)
rMergeSort(A, m+1, r)
merge(A, l, m, r)
2. returnAlg merge(A, l, m, r)
input sorted array A[l..m], A[m+1..r]
output sorted array A[l..r] merged from A[l..m] and A[m+1..r]
1. i, k <- l
2. j <- m+1
3. while (i <= m & j <= r)
if (A[i] <= A[j])
B[k++] <- A[i++]
else
B[k++] <- A[j++]
4. while (i <= m)
B[k++] <- A[i++]
5. while (j <= r)
B[k++] <- A[j++]
6. for k <- l to r
A[k] <- B[k]
7. return
퀵 정렬
- 분할통치법에 기초한 정렬 알고리즘
- 분할(divide): 기준원소 p(pivot, 보통은 마지막 원소)를 택하여 L을 다음 세 부분으로 분할
- LT (p보다 작은 원소들)
- EQ (p와 같은 원소들)
- GT (p보다 큰 원소들)
- 재귀(recur): LT와 GT를 정렬
- 통치(conquer): LT, EQ, GT를 결합
- 분할(divide): 기준원소 p(pivot, 보통은 마지막 원소)를 택하여 L을 다음 세 부분으로 분할
Alg quickSort(L)
input list L with n elements
output sorted list L
1. if (L.size() > 1)
k <- a position in L
LT, EQ, GT <- partition(L, k)
quickSort(LT)
quickSort(GT)
L <- merge(LT, EQ, GT)
2. return
리스트 분할
- 입력 리스트를 다음과 같이 분할
- L로부터 각 원소 e를 차례로 삭제
- e를 기준원소 p와의 비교 결과에 따라 부리스트 LT, EQ, GT에 삽입
- 삽입과 삭제를 리스트의 맨앞이나 맨뒤에서 수행하므로 O(1) 소요
- 따라서, quick-sort의 분할 단계는 O(n) 시간 소요
Alg partition(L, k)
input list L with n elements,
position k of pivot
output sublists LT, EQ, GT of the elements of L,
less than, equal to, or greater than pivot, resp
1. p <- L.get(k)
2. LT, EQ, GT <- empty list
3. while (!L.isEmpty())
e <- L.removeFirst()
if (e < p)
LT.addLast(e)
elseif (e = p)
EQ.addLast(e)
else {e > p}
GT.addLast(e)
4. return LT, EQ, GT
기준원소 선택
- 리스트 원소 가운데 기준원소(pivot) 선택
- 결정적이며 쉬운 방법
- 맨 앞 원소
- 맨 뒤 원소
- 중간 원소
- 결정적이며 조금 복잡한 방법
- 맨 앞, 중간, 맨 뒤 위치의 세 원소의 중앙값(median)
- 0/4, 1/4, 2/4, 3/4, 4/4 위치의 다섯 원소의 중앙값
- 전체 원소의 중앙값
- 무작위한 방법
- 무작위 방식으로 원소 선택
- 결정적이며 쉬운 방법
- 기준원소 선택의 영향
- 분할 결과
- 퀵 정렬 수행 성능
퀵 정렬 트리
- quick-sort의 실행을 이진트리로 도식화
- 이진트리의 각 노드는 quick-sort의 재귀호출을 표현하며 다음을 저장
- 실행 이전의 무순 리스트 및 기준원소
- 실행 이후의 정렬 리스트
- 루트는 초기 호출을 의미
- 잎들은 크기 0 또는 1의 부리스트에 대한 호출을 의미
- 이진트리의 각 노드는 quick-sort의 재귀호출을 표현하며 다음을 저장
최악실행시간
- quick-sort의 최악은 기준원소가 항상 유일한 최소이거나 최대 원소일 경우
- 이 경우 LT와 GT 가운데 하나는 크기가 n-1이며, 다른 쪽의 크기가 0
- 실행시간은 다음 합에 비례: n + (n-1) + ... + 2 + 1
- 따라서, quick-sort의 최악실행시간: O(n^2)
기대실행시간
- 크기 s의 리스트에 대한 quick-sort의 재귀 호출을 고려하면,
- 좋은 호출: LT와 GT의 크기가 모두 (3/4)s 보다 작다.
- 나쁜 호출: LT와 GT의 가운데 하나의 크기가 (3/4)s 보다 크다.
- 호출이 좋을 확률은 1/2 (예: 동전던지기)
- 가능한 기준원소의 1/2은 좋은 호출을 부른다.
무작위 퀵 정렬
- quick-sort의 결정적 버전에서는, 기준원소로서 리스트로부터의 특정한 원소, 즉 마지막 원소를 선택하였다.
- 기준원소 선택을 위한 새로운 규칙
- 입력 리스트의 무작위(random) 원소를 선택하라
- 확률적 상식: k개의 헤드를 얻기 위한 동전던지기의 기대횟수는 2k이다.
무작위 퀵 정렬의 기대실행시간
- 깊이 i의 노드에 대해 다음을 기대할 수 있다.
- i/2개의 조상: 좋은 호출
- 현재 호출을 위한 입력 리스트의 크기: 최대 (3/4)^(i/2) * n
- 따라서,
- 깊이 2log4/3 (n)의 노드에 대해, 기대 입력 크기: 1
- 퀵 정렬 트리의 기대 높이: O(log n)
- 같은 깊이의 노드들에 대해 수행되는 작업량: O(n)
- 따라서, quick-sort의 기대실행시간 O(nlog n)
제자리 퀵 정렬
- quick-sort를 제자리에서 수행되도록 구현 가능
- 분할 단계에서, 입력 리스트의 원소들을 재배치하기 위해 대체(replace) 작업을 사용
- LT (a보다 아래의, 기준원소보다 작은 원소들)
- EQ (a와 b 사이의, 기준원소와 같은 원소들)
- GT (b보다 위의, 기준원소보다 큰 원소들)
- 재귀호출은 LT와 GT 부리스트에 대해 수행
Alg inPlaceQuickSort(L, l, r)
input list L, position l, r
output list L with elements of position from l to r rearranged in increasing order
1. if (l >= r)
return
2. k <- a position between l and r
3. a, b <- inPlacePartition(L, l, r, k)
4. inPlaceQuickSort(L, l, a-1)
5. inPlaceQuickSort(L, b+1, r)
제자리 분할
Alg inPlacePartition(A, l, r, k)
input array A[l..r] of distinct elements, index l, r, k
output final index of the pivot resulting from partitioning A[l..r] into LT, pivot, GT
1. p <- A[k] {pivot}
2. A[k] <-> A[r] {hide pivot}
3. i <- l
4. j <- r-1
5. while (i <= j)
while (i <= j & A[i] <= p)
i <- i+1
while (j >= i & A[j] >= p)
j <- j-1
if (i < j)
A[i] <-> A[j]
6. A[i] <-> A[r]
7. return i {index of pivot}- 위의 inPlacePartition 버전은 입력 배열 A가 유일한 원소로만 이루어졌다고 전제한 것이다.
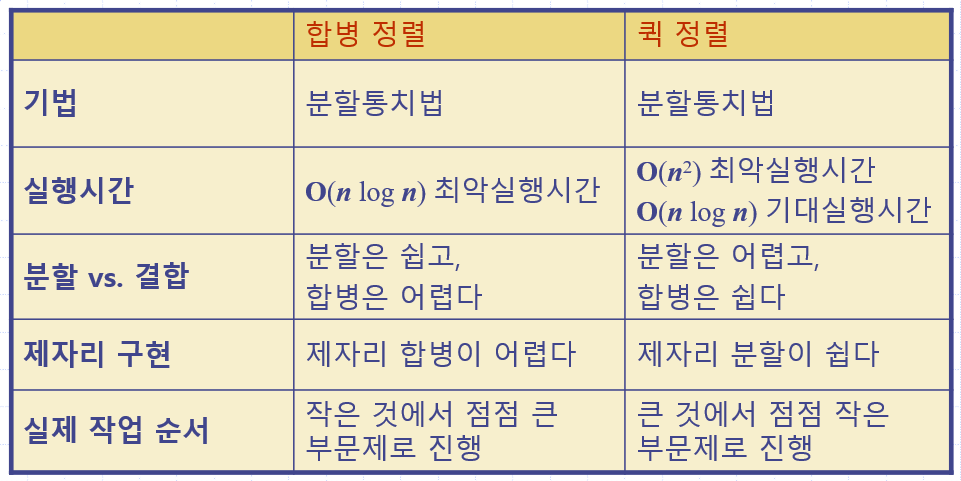
합병 정렬과 퀵 정렬 비교
분할통치법 (divide-and-conquer)
- 일반적인 알고리즘 설계 기법의 일종
- 분할 (divide): 입력 데이터 L을 둘 이상의 분리된 부분집합 L1, L2, ... 으로 나눔
- 재귀 (recur): L1, L2, ... 각각에 대한 부문제를 재귀적으로 해결
- 통치 (conquer): 부문제들에 대한 해결을 합쳐 L의 해결을 구함
- 재귀의 베이스 케이스: 상수 크기의 부문제들
- 점화식 (recurrence equations)을 사용하여 분석
- ex) 합병 정렬 (merge-sort), 퀵 정렬 (quick-sort)
합병 정렬
- 합병 정렬 (merge-sort): 분할통치법에 기초한 정렬 알고리즘
- 힙 정렬(heap-sort)처럼
- 비교에 기초한 정렬
- O(nlogn) 시간에 수행
- 힙 정렬(heap-sort)과는 달리
- 외부의 우선순위 큐를 사용하지 않음
- 데이터를 순차적 방식으로 접근 (따라서 디스크의 데이터를 정렬하기에 적당)
- n개의 원소로 이루어진 입력 리스트 L에 대한 합병 정렬 (merge-sort)의 세 단계
- 분할 (divide): 무순리스트 L을 각각 n/2개의 원소를 가진 두 개의 부리스트 L1과 L2로 분할
- 재귀 (recur): L1과 L2를 각각 재귀적으로 정렬
- 통치 (conquer): L1과 L2를 단일 순서리스트로 합병
Alg mergeSort(L)
input list L with n elements
output sorted list L
1. if (L.size() > 1)
L1, L2 <- partition(L, n/2)
mergeSort(L1)
mergeSort(L2)
L <- merge(L1, L2)
2. return
두 개의 정렬 리스트 합병하기
- merge-sort의 통치 단계: 두 개의 정렬된 리스트 L1과 L2를 L1과 L2의 원소들의 합을 포함하는 정렬 리스트 L로 합병하는 과정
- 각각 n/2개의 원소를 가지며, 이중연결리스트로 구현된 두 개의 정렬 리스트를 합병하는데 O(n) 시간 소요
Alg merge(L1, L2)
input sorted list L1 and L2 with n/2 elements each
output sorted list of L1 U L2
1. L <- empty list
2. while (!L1.isEmpty() & !L2.isEmpty())
if (L1.get(1) <= L2.get(1))
L.addLast(L1.removeFirst())
else
L.addLast(L2.removeFirst())
3. while (!L1.isEmpty())
L.addLast(L1.removeFirst())
4. while (!L2.isEmpty())
L.addLast(L2.removeFirst())
5. return L
합병정렬 트리
- merge-sort의 실행을 이진트리로 도식화
- 이진트리의 각 노드는 merge-sort의 재귀호출을 표현하며 다음을 저장
- 실행 이전의 무순리스트 및 분할
- 실행 이후의 정렬리스트
- 루트는 초기 호출을 의미
- 잎들은 크기 1의 부리스트에 대한 호출을 의미
- 이진트리의 각 노드는 merge-sort의 재귀호출을 표현하며 다음을 저장
합병 정렬 분석
- 합병 정렬 트리의 높이 h: O(log n)
- 각 재귀호출에서 리스트를 절반으로 나누기 때문
- 깊이 i의 노드들에서 이루어지는 총 작업량: O(n)
- 2^i개의 크기 n/(2^i)의 리스트들을 분할하고 합병하기 때문
- 2^(k+1)번의 재귀호출 발생
- 따라서, merge-sort의 전체 실행시간: O(nlog n)
- 점화식으로도 해결 가능
- T(n) = c (n < 2)
- T(n) = 2T(n/2) + O(n) (n >= 2)
- 전체 실행시간: T(n) = O(nlog n)
배열에 대한 합병 정렬
- 배열에 대해 작동하는 merge-sort 알고리즘
- mergeSort(A): n개의 원소로 구성된 배열 A를 합병 정렬
- 힌트: 외부 배열을 "버퍼", 즉 임시 저장 공간으로 사용
Alg mergeSort(A)
input array A of n keys
output sorted array A
1. rMergeSort(A, 0, n-1)
2. returnAlg rMergeSort(A, l, r)
input array A[l..r]
output sorted array A[l..r]
1. if (l < r)
m <- floor((l+r)/2)
rMergeSort(A, l, m)
rMergeSort(A, m+1, r)
merge(A, l, m, r)
2. returnAlg merge(A, l, m, r)
input sorted array A[l..m], A[m+1..r]
output sorted array A[l..r] merged from A[l..m] and A[m+1..r]
1. i, k <- l
2. j <- m+1
3. while (i <= m & j <= r)
if (A[i] <= A[j])
B[k++] <- A[i++]
else
B[k++] <- A[j++]
4. while (i <= m)
B[k++] <- A[i++]
5. while (j <= r)
B[k++] <- A[j++]
6. for k <- l to r
A[k] <- B[k]
7. return
퀵 정렬
- 분할통치법에 기초한 정렬 알고리즘
- 분할(divide): 기준원소 p(pivot, 보통은 마지막 원소)를 택하여 L을 다음 세 부분으로 분할
- LT (p보다 작은 원소들)
- EQ (p와 같은 원소들)
- GT (p보다 큰 원소들)
- 재귀(recur): LT와 GT를 정렬
- 통치(conquer): LT, EQ, GT를 결합
- 분할(divide): 기준원소 p(pivot, 보통은 마지막 원소)를 택하여 L을 다음 세 부분으로 분할
Alg quickSort(L)
input list L with n elements
output sorted list L
1. if (L.size() > 1)
k <- a position in L
LT, EQ, GT <- partition(L, k)
quickSort(LT)
quickSort(GT)
L <- merge(LT, EQ, GT)
2. return
리스트 분할
- 입력 리스트를 다음과 같이 분할
- L로부터 각 원소 e를 차례로 삭제
- e를 기준원소 p와의 비교 결과에 따라 부리스트 LT, EQ, GT에 삽입
- 삽입과 삭제를 리스트의 맨앞이나 맨뒤에서 수행하므로 O(1) 소요
- 따라서, quick-sort의 분할 단계는 O(n) 시간 소요
Alg partition(L, k)
input list L with n elements,
position k of pivot
output sublists LT, EQ, GT of the elements of L,
less than, equal to, or greater than pivot, resp
1. p <- L.get(k)
2. LT, EQ, GT <- empty list
3. while (!L.isEmpty())
e <- L.removeFirst()
if (e < p)
LT.addLast(e)
elseif (e = p)
EQ.addLast(e)
else {e > p}
GT.addLast(e)
4. return LT, EQ, GT
기준원소 선택
- 리스트 원소 가운데 기준원소(pivot) 선택
- 결정적이며 쉬운 방법
- 맨 앞 원소
- 맨 뒤 원소
- 중간 원소
- 결정적이며 조금 복잡한 방법
- 맨 앞, 중간, 맨 뒤 위치의 세 원소의 중앙값(median)
- 0/4, 1/4, 2/4, 3/4, 4/4 위치의 다섯 원소의 중앙값
- 전체 원소의 중앙값
- 무작위한 방법
- 무작위 방식으로 원소 선택
- 결정적이며 쉬운 방법
- 기준원소 선택의 영향
- 분할 결과
- 퀵 정렬 수행 성능
퀵 정렬 트리
- quick-sort의 실행을 이진트리로 도식화
- 이진트리의 각 노드는 quick-sort의 재귀호출을 표현하며 다음을 저장
- 실행 이전의 무순 리스트 및 기준원소
- 실행 이후의 정렬 리스트
- 루트는 초기 호출을 의미
- 잎들은 크기 0 또는 1의 부리스트에 대한 호출을 의미
- 이진트리의 각 노드는 quick-sort의 재귀호출을 표현하며 다음을 저장
최악실행시간
- quick-sort의 최악은 기준원소가 항상 유일한 최소이거나 최대 원소일 경우
- 이 경우 LT와 GT 가운데 하나는 크기가 n-1이며, 다른 쪽의 크기가 0
- 실행시간은 다음 합에 비례: n + (n-1) + ... + 2 + 1
- 따라서, quick-sort의 최악실행시간: O(n^2)
기대실행시간
- 크기 s의 리스트에 대한 quick-sort의 재귀 호출을 고려하면,
- 좋은 호출: LT와 GT의 크기가 모두 (3/4)s 보다 작다.
- 나쁜 호출: LT와 GT의 가운데 하나의 크기가 (3/4)s 보다 크다.
- 호출이 좋을 확률은 1/2 (예: 동전던지기)
- 가능한 기준원소의 1/2은 좋은 호출을 부른다.
무작위 퀵 정렬
- quick-sort의 결정적 버전에서는, 기준원소로서 리스트로부터의 특정한 원소, 즉 마지막 원소를 선택하였다.
- 기준원소 선택을 위한 새로운 규칙
- 입력 리스트의 무작위(random) 원소를 선택하라
- 확률적 상식: k개의 헤드를 얻기 위한 동전던지기의 기대횟수는 2k이다.
무작위 퀵 정렬의 기대실행시간
- 깊이 i의 노드에 대해 다음을 기대할 수 있다.
- i/2개의 조상: 좋은 호출
- 현재 호출을 위한 입력 리스트의 크기: 최대 (3/4)^(i/2) * n
- 따라서,
- 깊이 2log4/3 (n)의 노드에 대해, 기대 입력 크기: 1
- 퀵 정렬 트리의 기대 높이: O(log n)
- 같은 깊이의 노드들에 대해 수행되는 작업량: O(n)
- 따라서, quick-sort의 기대실행시간 O(nlog n)
제자리 퀵 정렬
- quick-sort를 제자리에서 수행되도록 구현 가능
- 분할 단계에서, 입력 리스트의 원소들을 재배치하기 위해 대체(replace) 작업을 사용
- LT (a보다 아래의, 기준원소보다 작은 원소들)
- EQ (a와 b 사이의, 기준원소와 같은 원소들)
- GT (b보다 위의, 기준원소보다 큰 원소들)
- 재귀호출은 LT와 GT 부리스트에 대해 수행
Alg inPlaceQuickSort(L, l, r)
input list L, position l, r
output list L with elements of position from l to r rearranged in increasing order
1. if (l >= r)
return
2. k <- a position between l and r
3. a, b <- inPlacePartition(L, l, r, k)
4. inPlaceQuickSort(L, l, a-1)
5. inPlaceQuickSort(L, b+1, r)
제자리 분할
Alg inPlacePartition(A, l, r, k)
input array A[l..r] of distinct elements, index l, r, k
output final index of the pivot resulting from partitioning A[l..r] into LT, pivot, GT
1. p <- A[k] {pivot}
2. A[k] <-> A[r] {hide pivot}
3. i <- l
4. j <- r-1
5. while (i <= j)
while (i <= j & A[i] <= p)
i <- i+1
while (j >= i & A[j] >= p)
j <- j-1
if (i < j)
A[i] <-> A[j]
6. A[i] <-> A[r]
7. return i {index of pivot}- 위의 inPlacePartition 버전은 입력 배열 A가 유일한 원소로만 이루어졌다고 전제한 것이다.
합병 정렬과 퀵 정렬 비교

